今日の授業について
今日の授業は前回の授業の続きになります。前回の授業は下記を参照してください。

前回の授業では「10のまとまり」を崩すことで、繰り下がりがある計算ができるということを意識させる授業を行いました。引けるものを先に引いてから、残りを、10から引く方法である「減減法」と10から一の位を引いてから、残ったものを足す「減加法」の2通りのやり方に注目していく活動を行いました。
本日の授業 1年生算数「繰り下がりのある引き算〜2つのやり方に注目してみよう〜」
授業のポイント
- 繰り下がりの計算をするときには、2種類の方法があるということに気づく。
- 減減法・減加法のどちらでも計算ができるようにする。
- 自分のやりやすい方法で計算ができるようになる。
導入
前回で繰り下がりの仕組みをやったので、今回は、自分たちでブロックを使って作業をさせることからはじめました。

さて、前回はスライムたちがお散歩している話から計算をしていったよね。
それじゃあ、今日はそれをもとに、計算の仕方を考えていこうか。
まずはブロックを15個出して「並べて」みて!

はーい!並べました!
大体の子が、下の2通りと同じように並べていました。

ならべました!
□□□□□□□□□□ □□□□□

私もできました!
□□□□□□□□□□
□□□□□

並べられたね!ちょっと並べ方が人によって違うけれど似たような並べ方をしているね。どうしてそうやってならべたの?

10のまとまりがあるとわかりやすいからです!
展開

そうだね!それじゃあ、そこから、9個のブロックを取ってみよう!どうやって取っていくとわかりやすく取れるかな?
様々な考え方が出てきましたが、そのうちの一人のFさんの考え方に注目してみました。

私は、こう並んでいるところから
□□□□□□■■■■ □□□□□
こう並べ替えて9個のブロックを取りました!
□□□□□□ ■■■■□□□□□
(動かしたブロックを■で表しました。実際の授業では、手元をカメラで映し出して、実際に動かしている様子を見せました。)

どうして、そうやってみたのかな?

9個取らなきゃいけないけれど、右には5個のブロックがあるから、10からあと4個持ってきて、5に足して9にしました!
まずは前回確認した、減減法の考え方である、5を取って、残りの4を取る考え方が出てきました。
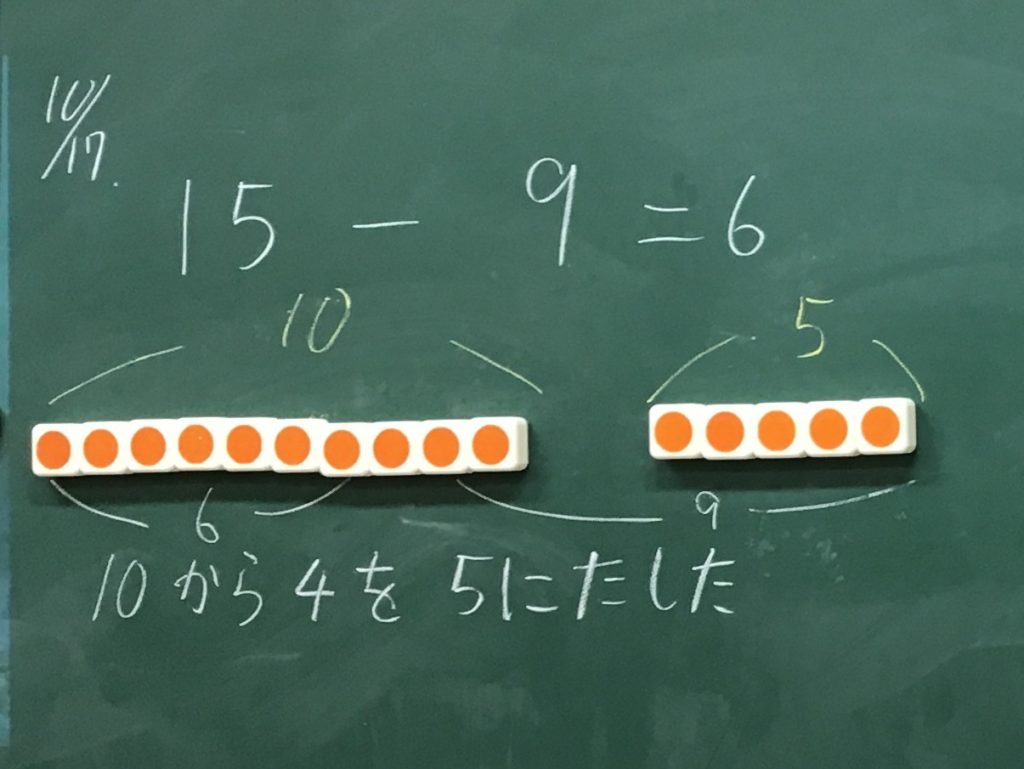

そうだね、これは昨日やった形だよね。先に、5個までは取れるから、あといくつを10から取れば良いのかな?ということを考えるとこうなるよね。
これを式にしてみようか!
そういって、黒板に式を書いていきました。
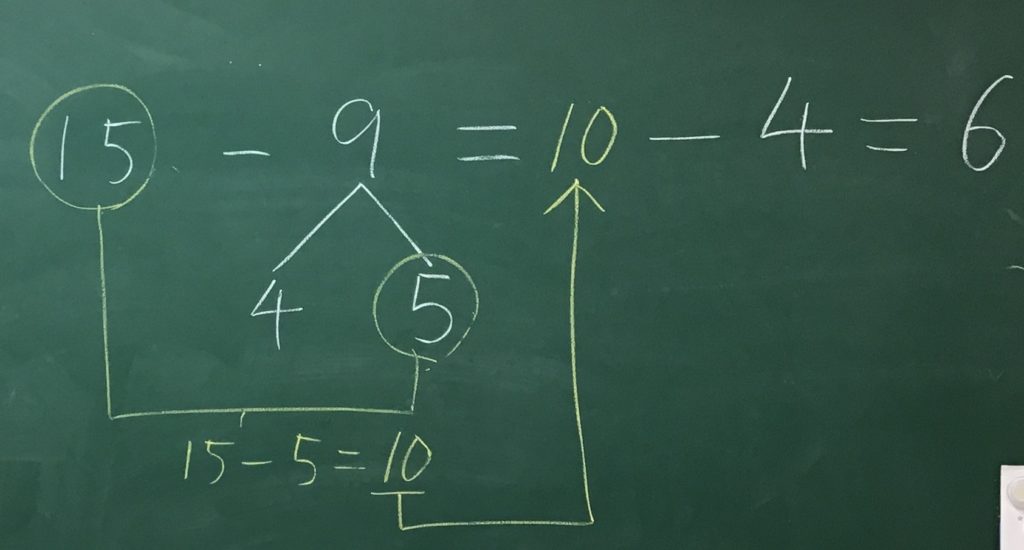

9を4と5に分けて、引きやすい5を先に引こう!そうするといくつになるかな?

10です!

そしてまだ引いてない数字は?

4です!

それじゃあ10から残りの4を引こうか!

できた!答えは6です!

ばっちり!これで引き算できたね!
次は減加法を取り上げていおくと思います。

今、5にあと4つくっつけて、9を作るという方法で9個取ったけれど、一度に9個全部取れる方法はないかな?
今度はAくんが答えてくれました。

できます!こうすればいいです!
ここから
□■■■■■■■■■ □□□□□
こうします!
□ □□□□□
■■■■■■■■■
(先ほどと同じで動かしたブロックを■で表しました。)


どうしてそうやってみたの?

だって、5から9は取れないけど、10からだったら9個取ることができるんだもん!

そっか、それで、9個取った後はどうするの?

10から9個取った残りの1個と5個をくっつけます!

よし、それじゃあ今度はそれを式にしてみよう!
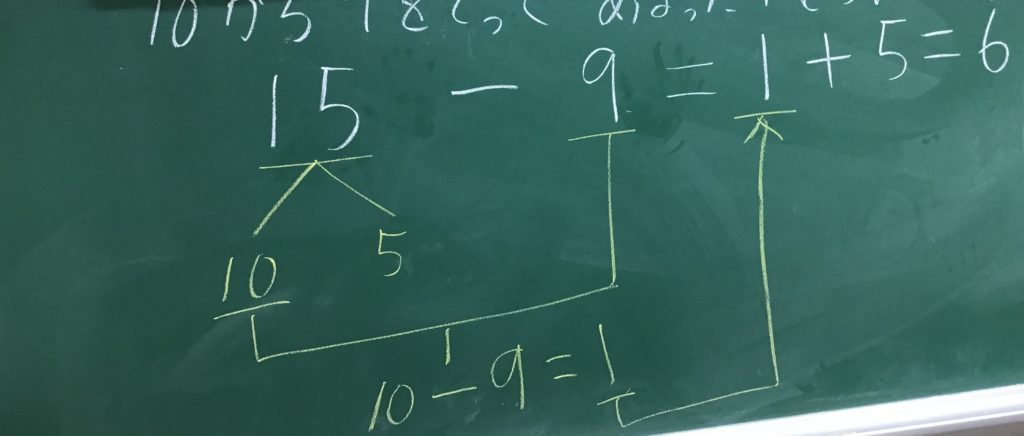

15のなかの10から、9を取るんだよね。ということは15を10と何にすればいいのかな?

10と5にすればいいです!

そうだね!そして、10から9を引くと、いくつ残った?

1です!

それで、全部でいくつ残っていることになるの・・・?

1個残っていて、さっき分けた5個を足さなきゃいけないから・・・1+5で6だ!

うん!さっきと同じ6になったね!引き算は2回引き算をしてもいいし、引き算をした後足し算をしても答えは出すことができるんだよ。その時によってやりやすいやり方でできるといいね!

同じ引き算なのに、違うやり方ができるんだね~
こうして、減減法と減加法を指導して終えました。
板書
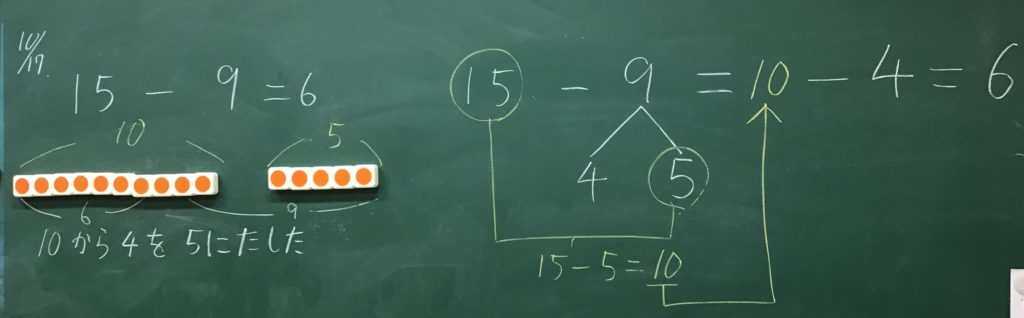

最後に
前回の授業で、「繰り下がりの仕組み」と必要性について指導をしていきました。そのため、今回は実際に計算する上でどのように計算をすればよいのか、考えていきました。
繰り下がりのある引き算は減減法と減加法の2種類の解き方がありますが、同じ答えにたどり着くために、複数の解き方があるということが特徴だと思います。
1年生の内容だと、複数のやり方で解くことができるものはそこまで多くないので、やり方の違いはあれど、一つの答えにたどり着くという算数の良さに注目できる良い教材ではないかなと思います。
それでは 本日の記事はここまでです。 それではいつものように、今回の記事が参考になったと思われた方、応援してくれる方は、励みになりますので、facebookやtwitterでのリンクのシェアをお願いします。
また、関連記事などもありますので見てもらえると大変嬉しいです。それではここまで読んでいただき、本当にありがとうございました。
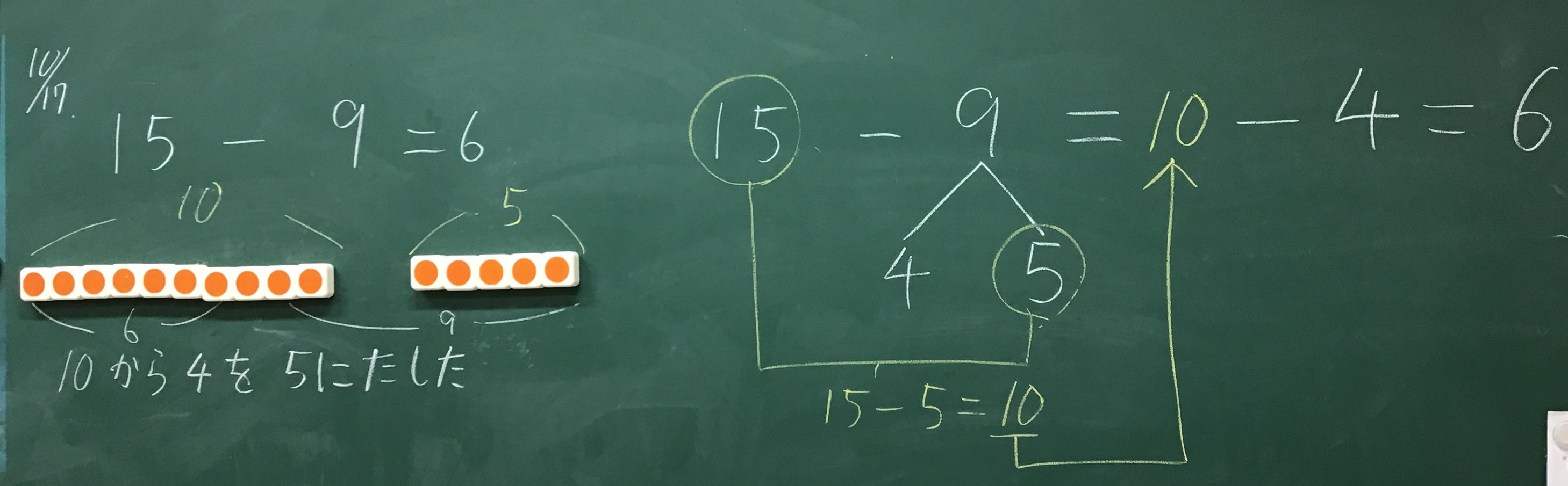






コメント