今日の授業について
本日の投稿は、本日の授業といいながら、本日行った授業ではありません(笑)
ブログ開設以前に板書の撮影のみ行っており、記事にできていなかったものです。
本日は授業がなかったため、その内容をまとめていきたいと思います。
ひき算の中でも、特に求補について扱った授業です。
算数1年生「いろいろなひき算」
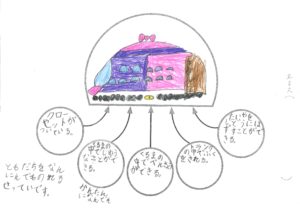
板書記録

今回の授業のポイント
ひき算の種類を捉えることができる。
- すでに、求差の問題は学習済みなので、場面が若干違うことに気づく
- 残りを出すひき算だけでなく、2つのものに分類するときも、ひき算を使うことができることがわかる
上記の2点をポイントとして捉えられるように授業をしていきました。
補足説明「求差」「求補」「求残」
よくかけ算で、「かける数」「かけられる数」の順序によって、意味合いが変わるということや交換法則が成り立つから、そこを区別する必要はないなどといった論争がありますが、意味合いが変わるという意味では、むしろひき算やたし算のほうが意味合いを捉える必要性があるのではないかなと考えています。
私自身、教員になってから改めて意識した話ですが、場面によって、どうしてひき算で計算すればよいのかというのはかわるのですよね。それが「求差」「求補」「求残」です。もうご存知の方は飛ばして読んでください。足し算についてはまたたし算の記事を書くときにそっと書く予定です。
「求差」:差を求めるために計算する
問題例 男の子5人と女の子3人います。どちらが何人多い?
「求残」:残りを求めるために計算する
問題例 5個のアメを持っていました。3個食べると残りは?
「求補」:2つの仲間に分けるために計算
問題例 白と黒のうさぎが5匹います。白のうさぎは3匹います。黒のうさぎは何匹いますか?
どれも、ひき算で求めますよね。式にしてしまうとどれも「5-3=2」と同じ式で表すことになります。そのように、簡略化して表すことができるのも算数や数学の利点ですよね。
導入
プロジェクターを使って、教科書の絵(板書記録のうさぎの絵)だけを映し出して、
「先生にはこの絵を見て、いくつか数字が見えるんだけど、みんなには見えるかな?」
と質問しました。絵を見て、何が何匹いるか捉えてほしかったからです。
すぐに思いつく人もいましたが、そうでない子も多かったので、続けて、
「例えばね、「8」という数字が先生には見えるんだよ」
と続けました。すると、「8」の数字がどこにあるのか、みんなが探し始めるようになりました。すぐに見つかったようで、はじめは見つけられなかった子も「よしっ」という顔になり、全員が見つけることができました。
「そのほかに、数字が見えた人はいる?」
と聞くと、すぐに
「3が見えます!」「5が見えます!」
と子どもたちが、数字を見つけてくれました。さて、数字を見つけたら次の段階です。
展開
「それでは、「8」と「5」と「3」の3つの数字を使って、引き算の式を作ってみましょう。」
次にこう子どもたちに発問しました。子どもたちはこの3つの数字を組み合わせて、うまく引き算の式を作ろうとします。しかし、ひき算の式が成立するのは「8ー3=5」と「8ー5=3」の2種類のみです。他の組み合わせを作ろうと試行錯誤していますが、はじめに5や3を入れるとどうしても成り立ちません。
少々余談になりますが・・・
ここで、はじめに3を入れて頑張ろうとしている人がいたので、クラスで取り上げてみました。3を入れると、どうしても引かれる数が、引く数よりも大きくなってしまいます。そのため引き算が(小学校段階では)成り立たなくなってしまいます。それにも子どもたちはすぐに気づくことができたので、改めて「引かれる数」は「引く数」よりも大きくないといけないという確認がみんなでできました。
また、「5-3=8」という意見がでてきたときに、「引き算じゃなければできるのにな~」という声があがったので、それを拾い、黒板に書いておきました。これが後に生きてくることになりました。
話は戻って、 「8ー3=5」と「8ー5=3」 の2つの式がでてきたあとに、もう一度、その数字を表す意味を考えてみました。
8 ー 3 = 5
すべてのうさぎ ー しろいうさぎ = くろいうさぎ
8 ー 5 = 3
すべてのうさぎ ー くろいうさぎ = しろいうさぎ
ここまで書くと、子どもたちも
「くろいうさぎとしろいうさぎがひっくり返っている!」
ということにすぐ気が付きました。どうしてひっくり返っているのか問うと、
「しろいうさぎとくろいうさぎさんは、別の子だから」
という意見がでてきました。
「その通り、今回は、「しろいうさぎだけ」にするか「くろいうさぎだけ」にするために、片方のうさぎを引き算していたんだよね。」
とまとめました。そして、前述した「足し算ならできるのに」という意見に戻り、
「それじゃあ足し算だったらできるのはなんでかな?」と前にだしたブロックをくっつけて、合わさる様子を見せながら聞くと
「別々にしたうさぎさんが、またもとに戻っている!」
ということにも気づくことができました。分けたうさぎは、足し算することでもとに戻せるという検算の話にもつながるところまで話を持っていくことができました。(検算についてはこの場では教えませんでしたが、いつか検算の話が出たときに今日の話をふと思い出してくれる子がいてくれたらいいなと勝手な願望として思っています。)
終わりに
今日の授業は、ひき算の中でも「求補」について取り上げていきました。正直大人になったり中学生で数学を習い始めると、むしろ意識をしなくなる部分だと思います。ですが、「算数」だからこそ、こういった現実に即した教え方と感覚を身に着けさせていけば、それが数学を学習し始めるときに生きてくるのではないかなと思います。
本日の記事はここまでです。 それではいつものように、 今回の記事が参考になったと思われた方、応援してくれる方は、励みになりますので、facebookやtwitterでのリンクのシェアをお願いします。 また、関連記事などもありますので見てもらえると大変嬉しいです。それではここまで読んでいただき、本当にありがとうございました。







コメント