今日の授業について
今日は教科書上巻の一番最後にある3つの数の計算を少し深めていくないようにとりくんでいきました。子どもたちからでてきた意見の中で「交換法則」につながる考え方が登場したので、そこをピックアップして授業を展開していきました。本来ここまで扱う予定はなかったのですが、子どもたちの発想から授業の深まりがでた授業になりました。
本日の授業 1年生 算数「3つの数の計算~計算の順序を変えてもいいの?~」
- たし算は順序を入れ替えても答えは変わらないことに気づく
- 「してもよい」「してはいけない」どちらかの立場にたち、自分の意見を持つことができる
導入
前回までに3つの数の計算の基本は抑えています。そのため、まずは復習から入りました。

さて、まずは前回の復習をしようか、この問題をやってみよう!
3+4+2=
この問題はみんなすぐ解くことができました。

答えは「9」です!

みんな計算早くなったね。それじゃあどのように考えて9という答えを出したか教えて下さい。
ここで、Oさんがこう答えてくれました。

はじめに、
①指で3を作りました。
②次に、4を足すから、左手に2個足して5にして、右手に残りの2を出し ました。
③最後に、2を足すと、9になりました。

具体的に説明をしてくれたね。それじゃあ、今Oさんが言ってくれた内容を式で表してくれる人はいるかな?
私が想定していた解答は「3+4」と「4+2」に分けて計算をしてくれるものでした。
ここで出た子どもたちからの解答は違うものでした。

5+4になります!
左手で表していた5と、右手で表していた4を足すという様子を式にしたことをいってくれました。

どうしてそう考えたの?

3と2をあわせて、5になっていたから、残ったものが4だから5+4だと思いました。
ここで、元の計画していた方向に戻しても良いかなと思ったのですが、「交換法則」の基本を学ぶ良いチャンスだと思い、授業の目的の方向転換をしました。

そっか~。そういう考えをしたんだね。でも一つ聞いていいかな?
3と2をあわせることになっているけれど、本当に3と2を先にあわせてもいいの?

えー、いいんじゃないの?

いや、でもだめかもしれないよ?

それじゃあ、ちょっと考えてみようか、「良いと思う」意見でもいいし、「だめと思う意見」でもいいから、隣の友だちと相談して、意見を出してみて!
そして、少し時間を取って、子どもたちに考えさせました。
板書

展開
話し合わせた後に、意見の集約をしました。

それじゃあ、「よいとおもういけん」でもいいし、「だめとおもういけん」でもいいので、意見をいってほしいな。
子どもたちは様々な意見をだしてくれました。
・算数の世界では、数字はいくつつなげてもいいから
・つなげないと足し算にならないから
・3+4+2の「4を2と2」に分けると、5+4になるから
これまで扱った算数の考え方を類推的に使ってくれる子が何人かいました。
・3+4+2の、「3と2」は離れているから足し算をしてはいけない
・3つの数の計算を2つにしてはいけないと思うから
・順番を守らないとごちゃごちゃになってしまうから
こういった意見が出てきました。
その意見に対して、反論や意見があるかと聞くと、Oくんがこんなことを言ってくれました。

ごちゃごちゃになってしまうという意見ですけど、
例えば「5+0+5」だと、ひっくり返しても同じなので、ごちゃごちゃにならないと思います。

でも今回は、3+4+2だよ?「5+0+5」は、反対から読んでも「5+0+5」になって同じです。
それだったら、2+4+3のときどうなるか考えたほうが良いと思います。

それだったら、2+3+4のときも考えてみたほうが良いんじゃないかな?

それじゃあ実際にやってみようか!
展開2
展開1の時点で授業が終わってしまったので、ここから先は次の授業の時に実施しました。
板書②
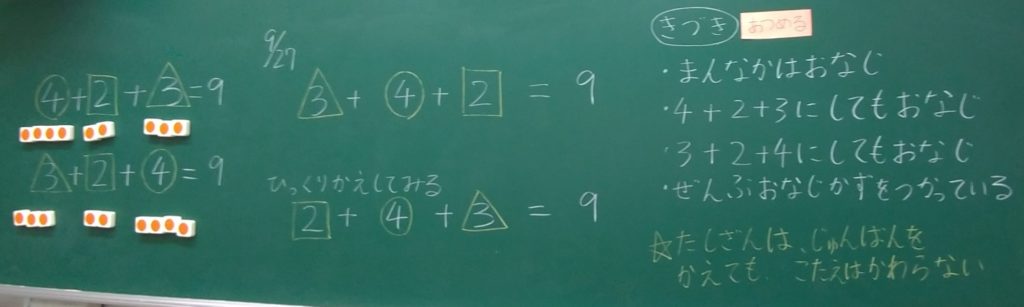

さて、ひっくり返してみたものを式として書いてみたけれど、どうかな?同じと言えそうかな。

答えは同じになりました!

それじゃあ、上の式と、下の式を見比べてみて、なにか気づいたことはあるかな?
はじめにKさんが答えてくれました。

真ん中はどっちも4になっています。

確かにそうだね。他になにかあるかな?
Yくんが今度は答えてくれました。

4が同じだけど、4を動かして、4+2+3でも同じになるんじゃないかなと思います。
今度はそれに伴って、他の人も言ってくれました。

それなら、3+2+4にしても同じじゃない?
そこで、それぞれを式にかいて、ブロックを動かし、答えを確認しました。

今4つの式がでてきたよね。この4つの式全てに共通することってなにかあるかな?

先生!全部同じ数字が使われています!

そうだね、ということはどういうことが言えそう?

足し算は、数字が同じであれば順番は変わっても答えは変わらないということが言えそうです!

そうだね!足し算は最終的にすべてを一緒にするから、どこから一緒にしても同じということがわかるね。だから、式でも順番は自由に入れ替えて計算をしてもいいんだよ。

それじゃあうまくやれば計算をしやすくできそうですね!

うん、これから上手く使ってみるといいね!
こうして2時間に渡った授業を終えました。
終わりに
今回は、3つの数の計算について取り扱っていきました。もともと、式を分割したものを扱うだけで終わりにしようと思っていたのですが、想定外の答えでは有りましたが、考えが深まりそうな答えがでたので、急遽そちらに方向を変えていく授業となりました。
目的は少し変わってしまいましたが、子どもたちはよい学びをすることができたのではないかと思います。
授業の展開を想定しておくことは大切ですが、子どもの実態や意見に合わせて柔軟に授業展開をしていくことの大切さを改めて感じました。
それでは 本日の記事はここまでです。 それではいつものように、今回の記事が参考になったと思われた方、応援してくれる方は、励みになりますので、もしよろしければfacebookやtwitterでのリンクのシェアをお願いします。
また、関連記事などもありますので見てもらえると大変嬉しいです。それではここまで読んでいただき、本当にありがとうございました。







コメント